The most common problem on developing a social network is, that you have to reflect a real world into the computer or more specific into the database. There are many nice things to work on, like finding the friend path to someone (to follow the theory, that everyone knows everyone on the earth over at most 6 edges), show friends of friends and the little more complex task of friend suggestion through a social graph.
I will treat these social mappings in later articles. For now we will concern on finding people near me under a territorial view. We could also say, finding locations near locations.
The main idea behind all of this is that you span a circle around a point on the map and search for all entities that will fall into that area. So what do we need? Think about a simple method to draw a circle or even better to get the distance between two points on the map. So we have our first optimization step, that we only check all entities against our fixed point on the map instead of really search in a circle. Let's go to the implementation of such a function in MySQL - we call it distance(), which will return the number of kilometers between two points:
CREATE FUNCTION distance(a POINT, b POINT) RETURNS double
DETERMINISTIC
RETURN ifnull(acos(sin(X(a)) * sin(X(b)) + cos(X(a)) * cos(X(b)) * cos(Y(b) - Y(a))) * 6380, 0);
There are many other approaches to get the distance between two points. But this function should be enough for the moment, especially under the view of performance. You will never need such a precision for this task, where you have to use the altitude or so. In the formula above the constant 6380 is the earth radius which is the main factor for the precision (because the earth is not a even ball), so play with that parameter at first, before you use a more complex algorithm like the Vincenty's formulae.
We could think about the solution like a simple circular area around a point:
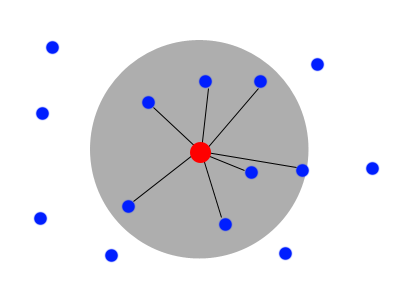
Let's write down a query to get all people near me:
SELECT *
FROM user
WHERE DISTANCE(geo_point, @my_pos) <= 15;
This looks good. But where is the problem? Right, MySQL doesn't have indexes on expressions, like Oracle for example. If you don't trust me, run EXPLAIN on that query. We could use a table, where we cache all distances between all peoples. The index would have a very good cardinality, because all distances of all peoples are given. But this is also the problem: "all peoples against all peoples" is similar to a cross join, which means the complexity of our table is n² to the number of users.
Okay what's next? We don't go over the peoples but rather over the locations. This number is fix and so we can cache it forever. Normally your location table looks like this:
CREATE TABLE IF NOT EXISTS `location` (
`id` smallint unsigned NOT NULL AUTO_INCREMENT,
`loc` varchar(48) NOT NULL,
`lat` double NOT NULL,
`lon` double NOT NULL,
PRIMARY KEY (`id`)
);
Every town, city or village has it's own entry in that table with a latitude and a longitude (yes, it's simplified). So how can we use this table to store all locations in the straight neighborhood? First we store the latitude and the longitude as a geometry object and than use another geometry column to store the "corners" of the circle. Corners of a circle? Yes, a circle can be approximated by reducing it's corners from infinite to let's say 1000. Because the calculation of 1000 corners needs also too much time, we reduce the number ones more to get a polygon with 24 or 12 corners, for example. So we will forget some people in the straight radius, but this is a sufficient approximation. To speed things up we also use the SPATIAL extension of MySQL here to use an R-Tree index for faster lookups on the geometry objects:
CREATE TABLE IF NOT EXISTS `location` (
`id` smallint unsigned NOT NULL AUTO_INCREMENT,
`label` varchar(48) NOT NULL,
`lat` double NOT NULL,
`lon` double NOT NULL,
`point` geometry NOT NULL,
`circle` geometry NOT NULL,
PRIMARY KEY (`id`),
SPATIAL KEY `point` (`point`),
SPATIAL KEY `circle` (`circle`)
);
Okay, so far so good. Now we have to fill the two new columns. First we fill our point geometry object from the lat and the lon...
UPDATE location SET point=GEOMFROMTEXT(CONCAT('POINT(', lat, ' ', lon, ')'));
...and then the column that will store our more complex geometry object as reference for our join
UPDATE location SET circle=GETPOLYGON(lat, lon, 15, 12);
What does this mean? We span a polygon over every location within a distance of 15 kilometers (like in the first approach using DISTANCE()) and we use 12 as number of corners of our polygon. Sure you could also use 1000 to make a more precise circle, but as I said, this slows things down and so I've limited it. The function GETPOLYGON() could be implemented as follows:
CREATE FUNCTION getpolygon(lat DOUBLE, lon DOUBLE, radius SMALLINT, corner TINYINT)
RETURNS geometry
DETERMINISTIC
BEGIN
DECLARE i TINYINT DEFAULT 1;
DECLARE a, b, c DOUBLE;
DECLARE res TEXT;
IF corner < 3 || radius > 500 THEN
RETURN NULL;
END IF;
SET res = CONCAT(lat + radius / 111.12, ' ', lon, ',');
WHILE i < corner do
SET c = RADIANS(360 / corner * i);
SET a = lat + COS(c) * radius / 111.12;
SET b = lon + SIN(c) * radius / (COS(RADIANS(lat + COS(c) * radius / 111.12 / 111.12)) * 111.12);
SET res = CONCAT(res, a, ' ', b, ',');
SET i = i + 1;
END WHILE;
RETURN GEOMFROMTEXT(CONCAT('POLYGON((', res, lat + radius / 111.12, ' ', lon, '))'));
END;
The view of our map has changed to:
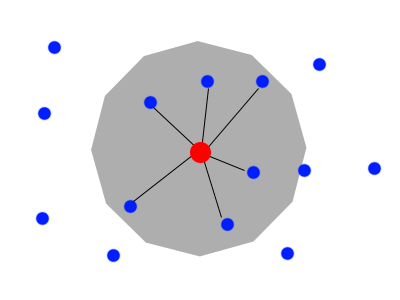
The last step is, to use our altered table :-)
SELECT B.*
FROM location A
JOIN location B ON CONTAINS(A.circle, B.point)
WHERE A.id=123
You have all locations within a radius of 15 kilometers in the result set. To use another distance, add a new column, or if you want to stagger it, add a new table circle_cache or something similar for that purpose.