Acm Solution: Turn All the Lights Off

Eshita is a very ecologically conscious person. She works late and every night before going home she makes sure that all the lights are turned off at her workplace to conserve electricity. The workplace is represented as a 2-dimensional grid. Each square in the grid has 4 neighbors in up, down, left and right directions. The electrical wiring is such that the sides of the grid wrap around i.e., the leftmost and the rightmost columns are neighbors. Similarly, the top and bottom rows are neighbors. This ensures that each of the squares in the grid has 4 neighbors.

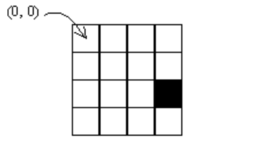
To standardize our notation, assume that the upper left-most square of the board is position \((0,0)\). Rows run horizontally and the top row is row 0. Columns are vertical and column 0 is the left-most column. Any reference to a square is by row then column; this square \((4,6)\) means row 4, column 6.

So, in the figure below, the grid has 4 columns and 4 rows (all the grids will have same number of rows and columns). The shaded square is denoted as \((2,3)\). The four neighbors of the square \((2,3)\) are squares \((1,3), (3,3), (2,2)\) and \((2,0)\). Similarly, the four neighbors of the square \((0,0)\) are squares \((3,0), (1,0), (0,1)\) and \((0,3)\).

Eshita is told that each square of the grid is a switch and a light. When a switch in some square is pushed, the light in that square and it's neighboring squares toggle their ON/OFF state. The next figure shows a sequence where, starting from a grid with all the lights OFF, switches \((1,1)\), and \((0,0)\) have been pushed. The ON lights are shown as shaded.

Given a grid with some of the lights ON, Eshita needs to say whether it is possible to turn all the lights OFF by pushing some sequence of button pushes. For example the first configuration of the 3x3 grid in the next figure, all the lights can be turned of by pushing switches \((0,0), (1,1)\) and \((2,2)\) (some other lights may be turned ON in the intermediate stages, but at the end of this sequence all the lights will be turned off). But in the second configuration, it is not possible to turn all the lights off by pushing any sequence of switches.

Your task is to write a program, which given some arbitrary configuration of a grid will determine whether all the lights can be turned off or not.

Input

The input file contains the description of several grids. Each grid starts with a line containing an integer size, specifying the number of rows and columns in the grid. Next line has a single integer \(n\), specifying the number of lights that are turned on. The following \(n\) lines contain two integers each, namely the row and column of each of ON light.

Output

For each of the grids output "Yes" or "No" on a line of its own. The output will be "Yes" if all the lights in the configuration can be turned off and "No" if it is not possible.

Sample Input

5
11
0 0
0 1
0 2
0 4
1 4
2 1
2 2
2 3
3 2
4 2
4 4
3
3
0 1
0 2
1 0

Sample Output

Yes
Now

Solution

Each switch only needs to be considered twice: pressed or not pressed. Pressing it twice cancels its effect, and the order of all presses is irrelevant. This turns the puzzle into arithmetic over \(\mathrm{GF}(2)\), where addition is XOR.

Number the \(s^2\) cells from \(0\) to \(s^2-1\). Let \(x_j\) indicate whether switch \(j\) is pressed, and let \(b_i\) be the initial state of light \(i\). The coefficient \(A_{ij}\) is one exactly when switch \(j\) toggles light \(i\). The required press pattern therefore satisfies

\[ A\mathbf{x}=\mathbf{b}\pmod 2. \]

This board wraps at every edge, so each matrix column marks the pressed cell and its four toroidal neighbors. The task asks only whether a solution exists, not which or how many switches to press. Consequently, no matrix inverse is required: Gaussian elimination on the augmented matrix \([A\mid\mathbf b]\) is enough. The board is impossible precisely when elimination produces a row whose coefficient side is all zero but whose right-hand side is one.

The general construction, including how a press vector can be recovered and why some boards have several solutions, is developed in the article on solving Lights Out using linear algebra. Here the implementation is limited to the consistency test needed by the problem.

const fs = require('fs');

function isSolvable(size, lights) {
  const cells = size * size;
  const matrix = Array.from({ length: cells }, () =>
    new Uint8Array(cells + 1)
  );

  const index = (row, column) =>
    ((row + size) % size) * size + ((column + size) % size);

  for (let row = 0; row < size; row++) {
    for (let column = 0; column < size; column++) {
      const press = index(row, column);
      for (const [dr, dc] of [[0, 0], [-1, 0], [1, 0], [0, -1], [0, 1]]) {
        matrix[index(row + dr, column + dc)][press] ^= 1;
      }
    }
  }

  for (const [row, column] of lights) {
    matrix[index(row, column)][cells] = 1;
  }

  let pivotRow = 0;
  for (let column = 0; column < cells && pivotRow < cells; column++) {
    let pivot = pivotRow;
    while (pivot < cells && matrix[pivot][column] === 0) pivot++;
    if (pivot === cells) continue;

    [matrix[pivotRow], matrix[pivot]] = [matrix[pivot], matrix[pivotRow]];
    for (let row = pivotRow + 1; row < cells; row++) {
      if (matrix[row][column] === 0) continue;
      for (let k = column; k <= cells; k++) {
        matrix[row][k] ^= matrix[pivotRow][k];
      }
    }
    pivotRow++;
  }

  return matrix.every((row) => {
    for (let column = 0; column < cells; column++) {
      if (row[column] !== 0) return true;
    }
    return row[cells] === 0;
  });
}

const values = fs.readFileSync(0, 'utf8').trim().split(/\s+/).map(Number);
let offset = 0;
const output = [];

while (offset < values.length) {
  const size = values[offset++];
  const count = values[offset++];
  const lights = [];

  for (let i = 0; i < count; i++) {
    lights.push([values[offset++], values[offset++]]);
  }

  output.push(isSolvable(size, lights) ? 'Yes' : 'No');
}

console.log(output.join('\n'));