The Goal
The goal for your program is to safely land the "Mars Lander" shuttle, the landing ship which contains the Opportunity rover. Mars Lander is guided by a program, and right now the failure rate for landing on the NASA simulator is unacceptable.
Note that it may look like a difficult problem, but in reality the problem is easy to solve. This puzzle is the first level among three, therefore, we need to present you some controls you won't need in order to complete this first level.
Note that it may look like a difficult problem, but in reality the problem is easy to solve. This puzzle is the first level among three, therefore, we need to present you some controls you won't need in order to complete this first level.
Rules
Built as a game, the simulator puts Mars Lander on a limited zone of Mars sky.
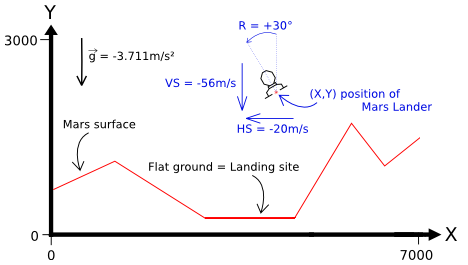
The zone is 7000m wide and 3000m high.
For this level, Mars Lander is above the landing zone, in vertical position, with no initial speed.
There is a unique area of flat ground on the surface of Mars, which is at least 1000 meters wide.
For this level, Mars Lander is above the landing zone, in vertical position, with no initial speed.
There is a unique area of flat ground on the surface of Mars, which is at least 1000 meters wide.
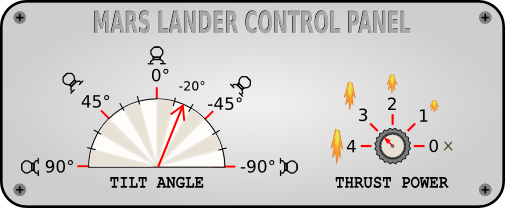
Angle goes from -90° to 90° . Thrust power goes from 0 to 4 .
For this level, you only need to control the thrust power: the tilt angle should be 0.
For this level, you only need to control the thrust power: the tilt angle should be 0.
For a landing to be successful, the ship must:
- land on flat ground
- land in a vertical position (tilt angle = 0°)
- vertical speed must be limited ( ≤ 40m/s in absolute value)
- horizontal speed must be limited ( ≤ 20m/s in absolute value)
Remember that this puzzle was simplified:
- the landing zone is just below the shuttle. You can therefore ignore rotation and always output 0 as the target angle.
- you don't need to store the coordinates of the surface of Mars to succeed.
- you only need your vertical landing speed to be between 0 and 40m/s – your horizontal speed being nil.
- As the shuttle falls, the vertical speed is negative. As the shuttle flies upward, the vertical speed is positive.
Note
For this first level, Mars Lander will go through a single test.
Tests and validators are only slightly different. A program that passes a given test will pass the corresponding validator without any problem.
Tests and validators are only slightly different. A program that passes a given test will pass the corresponding validator without any problem.
Game Input
The program must first read the initialization data from standard input. Then, within an infinite loop, the program must read the data from the standard input related to Mars Lander's current state and provide to the standard output the instructions to move Mars Lander.
Initialization input
Line 1: the number surfaceN of points used to draw the surface of Mars.
Next surfaceN lines: a couple of integers landXlandY providing the coordinates of a ground point. By linking all the points together in a sequential fashion, you form the surface of Mars which is composed of several segments. For the first point, landX = 0 and for the last point, landX = 6999
Next surfaceN lines: a couple of integers landXlandY providing the coordinates of a ground point. By linking all the points together in a sequential fashion, you form the surface of Mars which is composed of several segments. For the first point, landX = 0 and for the last point, landX = 6999
Input for one game turn
A single line with 7 integers: XYhSpeedvSpeedfuelrotatepower
- X,Y are the coordinates of Mars Lander (in meters).
- hSpeed and vSpeed are the horizontal and vertical speed of Mars Lander (in m/s). These can be negative depending on the direction of Mars Lander.
- fuel is the remaining quantity of fuel in liters. When there is no more fuel, the power of thrusters falls to zero.
- rotate is the angle of rotation of Mars Lander expressed in degrees.
- power is the thrust power of the landing ship.
Output for one game turn
A single line with 2 integers: rotatepower :
- rotate is the desired rotation angle for Mars Lander. Please note that for each turn the actual value of the angle is limited to the value of the previous turn +/- 15°.
- power is the desired thrust power. 0 = off. 4 = maximum power. Please note that for each turn the value of the actual power is limited to the value of the previous turn +/- 1.
Constraints
2 ≤ surfaceN < 30
0 ≤ X < 7000
0 ≤ Y < 3000
-500 < hSpeed, vSpeed < 500
0 ≤ fuel ≤ 2000
-90 ≤ rotate ≤ 90
0 ≤ power ≤ 4
Response time per turn ≤ 100ms
0 ≤ X < 7000
0 ≤ Y < 3000
-500 < hSpeed, vSpeed < 500
0 ≤ fuel ≤ 2000
-90 ≤ rotate ≤ 90
0 ≤ power ≤ 4
Response time per turn ≤ 100ms
JavaScript Solution
var N = parseInt(readline());
for (var i = 0; i < N; i++) {
var inputs = readline().split(' ');
}
while (true) {
var inputs = readline().split(' ');
var VS = parseInt(inputs[3]);
if (VS <= -40)
print('0 4');
else
print("0 0")
} All images are copyright to Codingame