Codesignal Solution: isTournament

Original Problem

Determine if the given directed graph is a tournament. A tournament is a directed graph in which every pair of distinct vertices is connected by a single directed edge.

Example

For
n = 5,
fromV = [2, 1, 3, 4, 4, 4, 1, 2, 3, 4] and
toV = [3, 2, 1, 3, 2, 1, 5, 5, 5, 5],
the output should be
isTournament(n, fromV, toV) = true.

Here's how the given graph looks like:

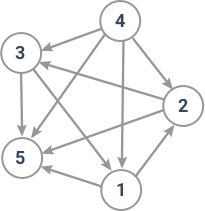
Input/Output

• [time limit] 4000ms (js)

• [input] integer n

  A positive integer n representing the number of vertices in the given graph.

  Guaranteed constraints:
  1 ≤ n ≤ 10.

• [input] array.integer fromV

  An array of integers containing integers less than or equal to n.

  Guaranteed constraints:
  0 ≤ fromV.length ≤ 50,
  1 ≤ fromV[i] ≤ n.

• [input] array.integer toV

  For each i in range [0, fromV.length)there is an edge from the vertex number fromV[i] to the vertex toV[i] in the given directed graph.

  Guaranteed constraints:
  toV.length = fromV.length,
  1 ≤ toV[i] ≤ n.

• [output] boolean

  true if the given graph is a tournament, false otherwise.

Solution

If we list all possible pairs of nodes for \(n=5\) and mark the ones for the given graph it may look like this:

(1, 1), <strong>(1, 2)</strong>, (1, 3), (1, 4), <strong>(1, 5)</strong><br />(2, 1), (2, 2), <strong>(2, 3)</strong>, (2, 4), <strong>(2, 5)</strong><br /><strong>(3, 1)</strong>, (3, 2), (3, 3), (3, 4), <strong>(3, 5)</strong><br /><strong>(4, 1)</strong>, <strong>(4, 2)</strong>, <strong>(4, 3)</strong>, (4, 4), <strong>(4, 5)</strong><br />(5, 1), (5, 2), (5, 3), (5, 4), (5, 5)

We now mirror the connections and see this nice pattern, where only the diagonal remains unmarked:

(1, 1), <strong>(1, 2)</strong>, <strong>(1, 3)</strong>, <strong>(1, 4)</strong>, <strong>(1, 5)</strong><br /><strong>(2, 1)</strong>, (2, 2), <strong>(2, 3)</strong>, <strong>(2, 4)</strong>, <strong>(2, 5)</strong><br /><strong>(3, 1)</strong>, <strong>(3, 2)</strong>, (3, 3), <strong>(3, 4)</strong>, <strong>(3, 5)</strong><br /><strong>(4, 1)</strong>, <strong>(4, 2)</strong>, <strong>(4, 3)</strong>, (4, 4), <strong>(4, 5)</strong><br /><strong>(5, 1)</strong>, <strong>(5, 2)</strong>, <strong>(5, 3)</strong>, <strong>(5, 4)</strong>, (5, 5)

Creating a set of unique connection tuples, is pretty straightforward using python3, by concatenating the two arrays \(f\) and \(t\). Duplicates get kicked out by the set creation: {*zip(f + t, f + t)}. Since the given constraints \(1 \leq f[i] \leq n\) and \(1 \leq t[i] \leq n\) all numbers are valid and we only need to work with the count. How many distinct tuples do we have? n-squared minus the diagonal. This allows us to implement the following routine:

isTournament = lambda n, f, t: len({*zip(f + t, t + f)}) == n * n - n

The routine would be perfectly small, but fails if the number is correct, but a duplicate connection gets removed. That's why we also need to check if the original length is okay to form the actual matrix:

isTournament = lambda n, f, t: len({*zip(f + t, t + f)}) == n * n - n and n * n - n == 2 * len(f)

Merging the two conditions to form a smaller solution yields the following final form:

isTournament = lambda n, f, t: n * n - n == 4 * len(f) + len({*zip(f + t, t + f)})

Using an adjacency matrix \(M\) we built before, we can solve the problem more elegantly by using an environment like Julia or Matlab:

isequal(M + M', 1 - eye(size(M)...))

All images are copyright to Codingame