The Goal
We can assume this network contains no cyclic relation.
For example, if person #1 has a relation with person #2 and if person #2 has a relation with person #3, then it is impossible for #3 to have a direct relation with #1. When an individual broadcasts a message, it is counted as a single step, meaning that the time it takes to broadcast the message is independant from the amount of people in direct relation with the individual. We will consider that this event will always take 1 hour. Here is an example with persons #1, #2, #3, #4, #5, #6, #7 and #8 linked like so:
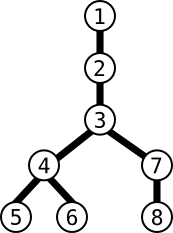
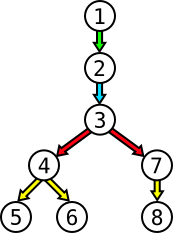
2. #2 then relays it to #3
3. #3 relays it to #4 and #7.
4. #4 relays it to #5 and #6, while #7 relays it to #8 If we decide now to start the propagation with person #3, then only 2 hours are needed:
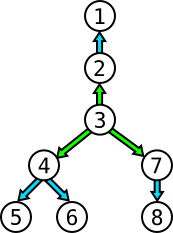
2. #2 relays it to #1 ; #4 relays it to #5 and #6 ; #7 relays it to #8 In this exercice, your mission consists in finding the minimal amount of hours it would take for a message to propagate across the entire network given to you as input.
Game Input
Line 1: N the number of adjacency relations.
N next lines: an adjancency relation between two people, expressed as X (space) Y, meaning that X is adjacent to Y.
0 ≤ X,Y < 200000
Solution
To solve this problem we need a way of identifying the most central element of the tree. Okay, in fact there is either one central vertex or two adjacent vertices, but this doesn't change much at the end.
The first idea was using a depth first search from a random vertex to find the most distant vertex. We now take the found vertex and search for the most distant vertex again. The traveled distance is the diameter of the tree and halving it results in the radius of the tree. The radius is exactly the value we're looking for in this problem. However, running two times a DFS on all nodes is computationally quite comprehensive.
The second idea is a bit different. We start by removing all leafs of the tree. We now remove all the leafs again and again, until only the center is remaining. Doing this is pretty efficient. However, removing elements from the adjacent list requires expensive array operations or even object re-creations. That's why I added a counter of adjacent vertices per node to reduce the amount of work to simple integer decrements. This allows to implement the algorithm like this:
var nodes = 0;
var depth = 0;
var counter = {};
var graph = {};
var n = +readline();
for (var i = 0; i < n; i++) {
var [xi, yi] = readline().split(' ').map(Number);
if (graph[xi] === undefined) graph[xi] = [], counter[xi] = 0, nodes++;
if (graph[yi] === undefined) graph[yi] = [], counter[yi] = 0, nodes++;
graph[xi].push(yi);
graph[yi].push(xi);
counter[xi]++;
counter[yi]++;
}
while (nodes > 2) {
// Create lists for delete elements
var delA = [];
var delB = [];
// Loop over all remaining nodes
for (var c in counter) {
// Skip if it's not a leaf
if (counter[c] !== 1)
continue;
// Scan over all neighbours of the leaf
for (var n of graph[c]) {
if (n in counter)
delA.push(n); // Mark neighbour as deleted (needs to be postponed since we loop over counter)
}
// Mark leaf to be deleted. This brings a huge performance benefit since the JS engine must copy counter
delB.push(c);
}
// Clean up marked vertices
for (var la of delA)
counter[la]--;
for (var la of delB)
delete counter[la], nodes--;
// Increment depth
depth++;
}
// If two nodes are remaining, we need one step more
if (nodes === 2)
depth++;
print(depth); All images are copyright to Codingame