The following undirected network consists of seven vertices and twelve edges with a total weight of 243.
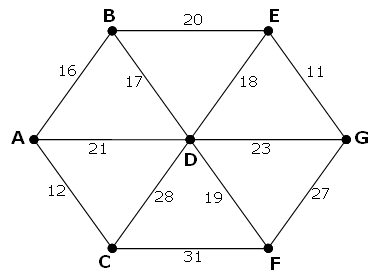
The same network can be represented by the matrix below.
| A | B | C | D | E | F | G | |
| A | - | 16 | 12 | 21 | - | - | - |
| B | 16 | - | - | 17 | 20 | - | - |
| C | 12 | - | - | 28 | - | 31 | - |
| D | 21 | 17 | 28 | - | 18 | 19 | 23 |
| E | - | 20 | - | 18 | - | - | 11 |
| F | - | - | 31 | 19 | - | - | 27 |
| G | - | - | - | 23 | 11 | 27 | - |
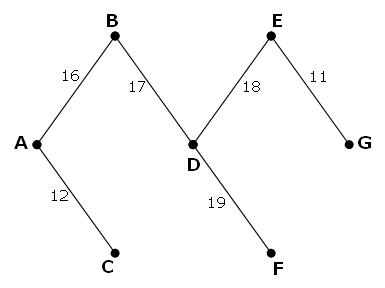
However, it is possible to optimise the network by removing some edges and still ensure that all points on the network remain connected. The network which achieves the maximum saving is shown below. It has a weight of 93, representing a saving of 243 − 93 = 150 from the original network.
Using network.txt (right click and 'Save Link/Target As...'), a 6K text file containing a network with forty vertices, and given in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected.
Solution
This problem is a perfect application of a minimum spanning tree, which is a tree connecting all vertices with the minimal edge cost. Solving the MST is conceptually easy using Tarjan's algorithm and computationally harder using Kruskal's or Prim's algorithm. Kruskal has the disadvantage that we need to sort the edges and find cycles within the graph. Prim's algorithm when implemented naively is even worse, but since we repeatedly have to find the edge with the minimum cost, we can store edges in a fibonacci heap.
We start with the boring part, reading in the matrix and storing it into an adjacency list. We sum over all existing matrix entries at the same time and divide by two afterwards, since we run over a symmetric matrix. To get the required maximum, we reduce this sum further by the cost of the MST:
#include <iostream>
#include <fstream>
#include <sstream>
#include <queue>
#include <climits>
int main() {
int numVertices = 40;
std::ifstream fs("p107_network.txt");
std::vector<std::pair<int, int> > graph[numVertices];
std::string line, field;
int sumCost = 0;
for (int i = 0; std::getline(fs, line); i++) {
std::istringstream s(line);
for (int j = 0; getline(s, field, ','); j++) {
if ("-" != field) {
int cost = std::atoi(field.c_str());
graph[i].push_back(std::make_pair(cost, j));
sumCost += cost;
}
}
}
fs.close();
std::cout << sumCost / 2 - costMST(graph, numVertices) << std::endl;
} But now to the interesting part, the function to calculate the actual cost of the remaining edges in the MST. We trick a bit with the heap by using the C++ priority_queue. We then start a loop in which we first add all unvisited neighbours to the priority queue and take the smallest edge out again to mark it visited and sum its cost. The algorithm implemented is pretty straightforward:
int costMST(std::vector<std::pair<int, int>> graph[], int numVertices) {
int sumCost = 0;
// Create a priority queue
std::priority_queue<std::pair<int, int>, std::vector <std::pair<int, int>>, std::greater<std::pair<int, int>>> queue;
std::vector<int> costs(numVertices, INT_MAX);
std::vector<bool> visited(numVertices, false);
int u = 0; // start node
queue.push(std::make_pair(0, u));
costs[u] = 0;
do {
// Traverse all adjacent nodes of u
for (auto x : graph[u]) {
int cost = x.first;
int v = x.second;
if (!visited[v] && cost < costs[v]) {
costs[v] = cost;
queue.push(std::make_pair(cost, v));
}
}
u = queue.top().second;
if (!visited[u]) {
visited[u] = true;
sumCost += queue.top().first;
}
queue.pop();
} while (!queue.empty());
return sumCost;
}