The Goal
You decide to take action by stopping Skynet from communicating on its own internal network.
Skynet's network is divided into several smaller networks, in each sub-network is a Skynet agent tasked with transferring information by moving from node to node along links and accessing gateways leading to other sub-networks.
Your mission is to reprogram the virus so it will sever links in such a way that the Skynet Agent is unable to access another sub-network thus preventing information concerning the presence of our virus to reach Skynet's central hub.
Rules
- A map of the network.
- The position of the exit gateways.
- The starting position of the Skynet agent.
Each game turn:
- First off, you sever one of the given links in the network.
- Then the Skynet agent moves from one Node to another accessible Node.
 Skynet agent |  Gateway |
Example
4 4 1
0 1
0 2
1 3
2 3
3 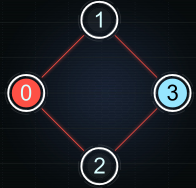
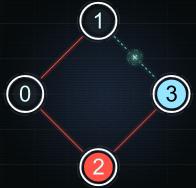
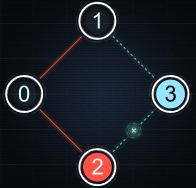
Note
Game Input
Line 1: 3 integers N L E
- N, the total number of nodes in the level, including the gateways.
- L, the number of links in the level.
- E, the number of exit gateways in the level.
Next L lines: 2 integers per line (N1, N2), indicating a link between the nodes indexed N1 and N2 in the network.
Next E lines: 1 integer EI representing the index of a gateway node.
1 ≤ L ≤ 1000
1 ≤ E ≤ 20
0 ≤ N1, N2 < N
0 ≤ SI < N
0 ≤ C1, C2 < N
Response time per turn ≤ 150ms
Solution
This problem is pretty simple, when it is only about cutting the way to a gateway. The game can be won just by cutting a random connection and only prevent the agent going to a gateway. However, another restriction is to have 50 or moves remaining. This brought me to elobarate several strategies. Here the ideas:
1. One improvement to the naiv random implementation is to try to encircle the agent by cutting the agents neighbours and intervene a gateway entering at the last resort
2. Another idea is to find the shortest path from the agent to the nearest gateway and cut either the last segment in front of the agent or the gate. For the shortest path, a lot of different algorithms can be used, like dijkstra's algorithm or a simple breadth first search.
3. A mere naiv idea is to cut all links from gateways to their direct neighbours as long as the agent isn't too close to a gateway. This could be improved by cutting a neighbour of the neighbours, closest to a gateway.
All these strategies have in common that they don't build a trap for the agent. When we observe the moving pattern, the agent always runs in circles. To improve the performance and not shut down so many links, we need to cut on the ring somewhere so that the agent runs in a trap. The basic idea builds on the previous strategies, but adds more heuristics.
4. We first check if the agent is close to a gateway and cut this link if necessary. Another heuristic is that we cut the link when the agent has two options to jump. We then cut the way with more neighbours behind. And the last step is building a trap. For the big games we have one move at the beginning, which is wasted with all other strategies, but for our optimal solution, we try to find a place to place it. When we look at the map, (almost) all nodes on rings have 3 neighbours, the gateway and the other two neighbours to the left and right. We focus on these 3 neighbour nodes, which are close to a gateway and search for their closest neighbour. It can happen that such a neighbour isn't present anymore. In this case we cut a random neighbour close to the agent. When it comes to the implementation, we read in the information into a simple graph strcuture:
var [N, L, E] = readline().split(' ').map(Number);
var graph = new Array(N);
var gates = new Array(E);
for (var i = 0; i < L; i++) {
var [N1, N2] = readline().split(' ').map(Number);
if (graph[N1] === undefined) graph[N1] = [];
if (graph[N2] === undefined) graph[N2] = [];
graph[N1].push(N2);
graph[N2].push(N1);
}
for (var i = 0; i < E; i++) {
gates[i] = +readline();
} And for the rest, we follow the previously described algorithm:
while (true) {
var SI = +readline();
var r1, r2 = SI;
// Check if agent neighbours are close to a gate
var neighbours = graph[SI];
var gate = neighbours.find(n => gates.indexOf(n) !== -1);
if (gate !== undefined) {
r1 = gate;
} else if (neighbours.length === 2) {
// If the agent has two options, cut the one with more neighbours
if (graph[neighbours[0]].length < graph[neighbours[1]].length) {
r1 = neighbours[1];
} else {
r1 = neighbours[0];
}
} else {
// Create a list of gate neighbours having 3 neighbours themselves
var gateNeighbours = [];
for (var g = 0; g < gates.length; g++) {
var gn = graph[gates[g]];
for (var n = 0; n < gn.length; n++) {
if (graph[gn[n]].length === 3) {
gateNeighbours.push(gn[n]);
}
}
}
// Take the first gate neighbour for the moment, could be improved
r1 = gateNeighbours[0];
// Cut on the ring to another neighbour
r2 = graph[r1].find(n => gateNeighbours.indexOf(n) !== -1);
if (r2 === undefined) {
r1 = neighbours[0];
r2 = SI;
}
}
graph[r1] = graph[r1].filter(x => x !== r2);
graph[r2] = graph[r2].filter(x => x !== r1);
print(r1 + ' ' + r2);
} All images are copyright to Codingame