Codingame Solution: Network Cabling

Original Problem

The Goal

Rules

For the implementation of the works, the operator has technical constraints whereby it is forced to proceed in the following manner:

A main cable will cross through the park from the West to the East (from the position x of the most westerly building to the position x of the most easterly building).

For each building, a dedicated cable will connect from the building to the main cable by a minimal path (North or South), as shown in the following example:

In this example, the green lines represent the cables.

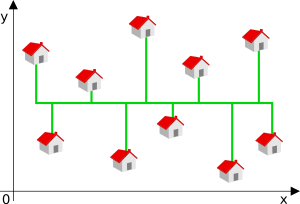
The minimum length will therefore depend on the position of the main cable.

Solution

That's a really interesting problem. For the horizontal distance it's easy, we need to find the left- and rightmost points. For the vertical position, we need to find the best height of the cable to minimize the distances. Least squares can't minimize the problem, think of the case when 3 houses are on one height and only one house is astray. The option that works is the minimum of the absolute values, or Manhatten distance, instead of least squares. But how can we minimize this? Interesting question. So interesting, I wrote an own article about the derivation. It's was astonishing, that it's the median of the values, which minimizes the absolute values. So all we have to do is run a hopefully minimalistic median implementation to solve this problem quickly. Here is my attemtp:

var minX = Infinity, maxX = 0, ys = [];
var minCable = 0;

var N = readline() | 0;

for (var i = 0; i < N; i++) {
    var inputs = readline().split(' ');
    var x = inputs[0] | 0;
    var y = inputs[1] | 0;
    
    maxX = Math.max(maxX, x);
    minX = Math.min(minX, x);

    ys.push(y);
}

ys.sort((a, b) => a - b);

var m = N % 2 
    ? ys[N >> 1]
    : Math.floor((ys[(N >> 1) - 1] + ys[N >> 1]) / 2)

for (var i = 0; i < N; i++) {
    minCable+= Math.abs(ys[i] - m);
}

print(minCable + maxX - minX);