The Goal
One part of this information is the list of TAN stops, timetables and routes. The region wants to provide TAN users with a tool which will allow them to calculate the shortest route between two stops using the TAN network.
Rules
The input data required for your program is provided in an ASCII text format:
- The stop which is the starting point of the journey
- The stop which is the final point of the journey
- The list of all the stops
- The routes between the stops
A series of lines representing the stops (one stop per line) and which contains the following fields:
- The unique identifier of the stop
- The full name of the stop, between quote marks"
- The description of the stop (not used)
- The latitude of the stop (in degrees)
- The longitude of the stop (in degrees)
- The identifier of the zone (not used)
- The url of the stop (not used)
- The type of stop
- The mother station (not used)
Example:
StopArea:ABDU,"Abel Durand",,47.22019661,-1.60337553,,,1, The routes between stops:
A list of lines representing the routes between the stops (one route per line). Each line contains two stop identifiers separated by a white space.
Each line represents a one-directional route running from the first identifier to the second. If two stops A and B are reciprocally accessible, then there will be two lines to represent this route:
A B
B A
Example:
StopArea:LAIL StopArea:GALH
StopArea:GALH StopArea:LAIL DISTANCE
The distance d between two points A and B will be calculated using the following formula:
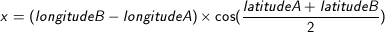
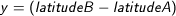
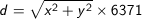
Note: the latitudes and longitudes are expressed in radians. 6371 corresponds to the radius of the earth in km.
The program will display the list of the full names of the stops along which the shortest route passes. If there is no possible route between the starting and final stops, the program will display IMPOSSIBLE.
Game Input
Line 1: the identifier of the stop which is the starting point of the journey
Line 2: the identifier of the stop which is the final point of the journey
Line 3: the number N of stops in the TAN network
N following lines: on each line a stop as described above
Following line: the number M of routes in the TAN network
M following lines: on each line a route as described above
If it is not possible to find a route between the start and end points, the program should display IMPOSSIBLE.
0 < M < 10000
Solution
We're given the distance measure based on a spherical earth projection, which can be implemented in JavaScript like this:
var dist = function(lat1, lon1, lat2, lon2) {
var x = (lon2 - lon1) * Math.cos(((lat1 + lat2) / 2));
var y = (lat2 - lat1);
return Math.sqrt(x * x + y * y) * 6371;
}; Since we need to find the shortest route based on the given measure, we need an algorithm to do this for us on a given graph. I think the best way to solve this problem is using an A*-algorithm. I think the implementation is pretty straightforward and for reusability, I implemented a little class called Graph:
function Graph() {
var info = {};
var map = {};
var H = null;
this.addEdge = function(node1, node2) {
if (map[node1] === undefined) {
map[node1] = [];
}
map[node1].push(node2);
};
this.addInfo = function(id, k, v) {
if (info[id] === undefined) {
info[id] = {};
}
info[id][k] = v;
};
this.setHeuristic = function(h) {
H = h;
};
this.getShortestPath = function(start, stop) { // A*
function path(P, current) {
var res = [
info[current]
];
while (current in P) {
current = P[current];
res.unshift(info[current]);
}
return res;
}
var closedset = [];
var openset = [start];
var came_from = {};
var g_score = {};
var f_score = {};
g_score[start] = 0;
f_score[start] = g_score[start] + H(info, start, stop);
while (openset.length > 0) {
// current := the node in openset having the lowest f_score[] value
var cur;
var min = f_score[openset[0]];
var min_i = 0;
for (var i = 1; i < openset.length; i++) {
if (min > f_score[openset[i]]) {
min = f_score[openset[i]];
min_i = i;
}
}
cur = openset[min_i];
if (cur === stop) {
return path(came_from, stop);
}
// remove current from openset
var index = openset.indexOf(cur);
if (index !== -1) {
openset.splice(index, 1);
}
//add current to closedset
closedset.push(cur);
var neighbors = map[cur];
for (var i = 0; i < neighbors.length; i++) {
var neighbor = neighbors[i];
// if neighbor in closedset
if (closedset.indexOf(neighbor) !== -1) {
continue;
}
var tentative_g_score = g_score[cur] + H(info, cur, neighbor);
if (-1 === openset.indexOf(neighbor) || tentative_g_score < g_score[neighbor]) {
came_from[neighbor] = cur;
g_score[neighbor] = tentative_g_score;
f_score[neighbor] = g_score[neighbor] + H(info, neighbor, stop);
if (-1 === openset.indexOf(neighbor)) {
openset.push(neighbor);
}
}
}
}
return null;
};
} The implementation isn't optimal, since the open set is scanned linearly. Using a heap structure would speed up things, but isn't needed for this problem though. Okay, using the Graph class, we can set up the heuristic and read in the data:
var G = new Graph;
G.setHeuristic(function(info, a, b) {
var lat1 = info[a].lat;
var lon1 = info[a].lon;
var lat2 = info[b].lat;
var lon2 = info[b].lon;
return dist(lat1, lon1, lat2, lon2);
});
function parseCoord(c) {
return parseFloat(c) / 180 * Math.PI;
}
var startPoint = readline();
var endPoint = readline();
var N = +readline();
for (var i = 0; i < N; i++) {
var stop = readline().split(",");
var id = stop[0];
G.addInfo(id, 'name', stop[1].slice(1, -1));
G.addInfo(id, 'lat', parseCoord(stop[3]));
G.addInfo(id, 'lon', parseCoord(stop[4]));
}
var M = parseInt(readline());
for (var i = 0; i < M; i++) {
var route = readline().split(" ");
G.addEdge(route[0], route[1]);
} Having set up the input processing and the graph implementation, the only thing needed is running the shortest path method and print out the path:
var nodes = G.getShortestPath(startPoint, endPoint);
if (nodes === null) {
print("IMPOSSIBLE");
} else {
for (var i = 0; i < nodes.length; i++) {
print(nodes[i].name);
}
} All images are copyright to Codingame